半球型类圆锥摆圆周运动模型

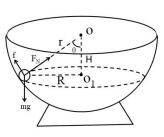
场景：如图所示，一质量为 m 的小球置于半径为 r 半球形容器内，小球对半球面的压力与竖直方向的夹角为θ，小球与半球形容器始终以相同的角速度绕中心线 OO’做水平匀速转动，动摩擦因数为μ。

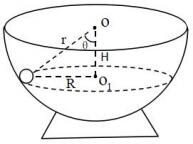
1、当μ=0 时，无论半圆形球的角速度多大均不影响小球的运动

受力特点：（如下图）

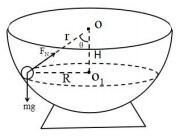
水平方向： FNsinθ=ma ①
竖直方向：Fcosθ=mg ②

动态分析

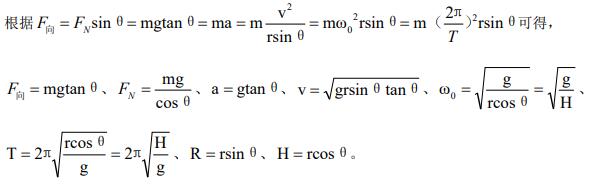
结论：
（1）当θ增大时， F向增加、 FN 增加、a 增加、v 增加、ω增加、R 增加、T 减小；
（2）小球的周期和角速度只与 H 和 g 有关，H 和 g 相同的不同半圆球周期和角速度相等；
（3）小球的加速度只与θ和 g 有关，g 相同时，θ越大、a 越大。

2、当μ≠0 时，半圆形球的角速度大小会影响小球的运动

（1）当 ω＞ωo时， FNsinθ＜mω²rsinθ，故故小球受到一沿切面向下的摩擦力 f

受力特点：（如下图）

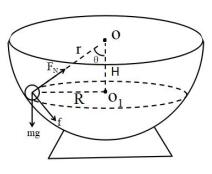
水平方向： FN sinθ+fcosθ=ma ③
竖直方向： FN cosθ – fsinθ=mg ④

动态分析：
联立③④解得： FN =mω²rsin²θ+mgcosθ⑦，f =mω²rsinθcosθ-mgsinθ⑧；

根据向心力公式得：F向 = mω²rsinθ、a = ω²rsinθ、v = ωrsinθ、 T=2π/ω 、R=rsinθ、 H=rcosθ。

即：
1）当θ不变，ω增大时：f 增大、 FN 增大、 F向增加、a 增加、v 增加、R 不变、H 不变、T 减
小；

（2）当 ω=ωo时， FNsinθ=mω²rsinθ，故不产生任何摩擦力，与μ=0 的情况相同；

（3）当 ω＜ωo时， FNsinθ＞mω²rsinθ，故小球受到一沿切面向上的摩擦力 f

受力特点：（如图）

水平方向： FN sinθ — fcosθ= ma ⑤
竖直方向： FNcosθ+ fsinθ=mg ⑥

动态分析：
联立⑤⑥解得： FN= mω²rsin2θ+ mgcosθ⑨，f =—mω²rsinθcosθ+ mgsinθ⑩；
根据向心力公式得：F向=mω²rsinθ、a = ω²rsinθ、v = ωrsinθ、 T=2π/ω 、R=rsinθ、 H=rcosθ。

即：
1）当θ不变，ω增大时： f 减小、 FN 增大、 F向增加、a 增加、v 增加、R 不变、H 不变、T减小；

故ω不变，θ增大时， f 减小、 FN 先增加后减小、 F向增加、a 增加、v 增加、R 增加、H 减小、T 不变。

球形圆锥圆周运动有关选择题

高中物理知识点总结

高中物理视频大全