
高中物理电学实验总是离不开电表,因而掌握电表的内部结构显得尤为重要。目前高中阶段所有接触的指针式电表均是由灵敏电流计(也称表头)改装过来的,比如电流表、电压表、欧姆表。特别说明一下,我们这里只讨论直流电表。作者:周小新(公众号:科学物理人)
表头的原理
所以我们一定要先说一下表头的原理。如下图是表头的内部结构,几个主要的结构是:磁铁、线圈、螺旋弹簧。
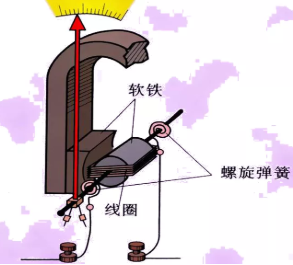
下图是灵敏电流计的的磁场分布情况(磁铁内部的磁感线未画出),常常称为均匀辐向磁场。画出来的这个磁场有什么特点呢?首先方向均指向(或背离)线圈的转轴,这就保证了线圈转到任意位置的时候,磁感线与线圈平面平行,保证线圈所受到的安培力垂直于线圈平面;然后就是与转轴距离相等的地方,磁感应强度大小一致。
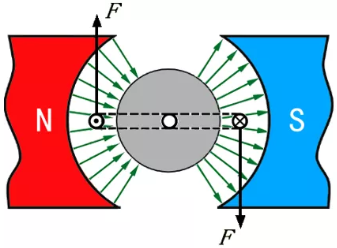
现在给线圈通上电流I,与磁感线垂直的那两条边(上图中打点和打叉的边)就会受到安培力的作用,如上图所示。图中F=NBIL1,其中N为线圈匝数、B为线圈所处位置的磁感应强度的大小、I为电流强度、L为受力边的长度。根据左手定则,很容易发现线圈受到的两个力方向如图所示,这两个力会产生一个什么效果呢?会让线圈转动起来,其实就是安培力的合力矩不等于零。
这个时候我们就要谈到结构中的螺旋弹簧的作用了。安培力想着让线圈转动起来,而螺旋弹簧就想着阻碍线圈转动。要度量这个转动效果,就要讲到力矩的概念,也就是当安培力的力矩与弹簧的力矩平衡时,线圈就不再转了(由于高中不要求掌握力矩的概念,其实就是初中学到的杠杆,动力×动力臂=阻力×阻力臂,我们的支点当然选择在转轴位置)。
对于安培力:动力×动力臂=2NBIL1×L2/2=NBIL1L2,(其中L2是受力边到转轴的距离);
对于弹簧:阻力×阻力臂=kθ,也就是这个阻力×阻力臂正比于扭转的角度,这已经超出了我们的能力范围,就不做解释了。
当NBIL1L2=kθ时,线圈就不再转动了,此时我们可以知道I=Cθ,C是一个常数,也就是说流过线圈的电流会正比于线圈转过的角度,其实也就是指针转过的角度,比例系数在制作表头的时候就可以算出来。那么,我们就可以通过指针偏转的角度来指示待测电流。当然,我们仔细看一下这个常数C,它与磁感应强度大小有关,我们之前说这个磁场是均匀辐向磁场,这自然直理想情况,实际上我们很难保证完全一样,通常中间部分会比较好,而边上通常会差一些,这也是为什么电学实验中常常要求指针偏转在1/3-2/3之间的原因,因为这个部分均匀辐向磁场还是比较理想的。
我们前面说到,我们讨论的指针式电表都是由表头改装过来的,那么我们应该注意,以后我们所有的电表指针的偏转角均直接反映的是流经表头的电流,这一点希望大家仔细体会。
其实上面说了这么多,如果你无法理解(比如你还没学到磁场),那么你只需要记住我们的结论就好。
下面我们要谈论的是表头的电路知识了。
从上面的讨论我们知道,表头本身是直接测量电流的,可是我们也知道线圈本身是有电阻的,那么自然表头上应该就是有电压的。
对于表头有Ug=IgRg,其中Ig为表头的满偏电流、Rg为表头内阻、Ug为表头的满偏电压。那么,实际上,表头本质上不仅仅是一个电流表,也是一个电阻,还是一个电压表。我们后面将讨论如何将表头改装成大量程的电流表和电压表,实际上核心还是表头。
顺便说一下,表头也称为灵敏电流计,主要原因是其满偏电流很小通常是微安级别(越小越灵敏),而其内阻通常较大,通常是千欧级别。大家如果平常注意观察,会发现,内阻越小的电表,通常满篇电流会大一些。
改装成大量程电压表
我们已经知道了,表头本质上也就是一个电压表,只不过其满偏电压比较小。我们需要获得大量程的电压表,怎么办呢?如果表头能够找到一个伙伴来分担一部分电压,那就好办了。不过事情还没完,表头还需要知道它的伙伴分担了多少电压,这样表头才能完成电压的测量。要同时完成这件事,要怎么办?
根据我们学过的知识,串联分压,如果找一个已知电阻与表头串联,这个电阻就可以分担一部分电压,又因为是串联的,表头知道它的伙伴身上的电压与它自己身上电压的比值,自然就完成了我们上面的任务。具体如下:
如下图,表头可以知道自己身上的电压,又知道伙伴身上的电压,那么总的待测电压自然而然就知道了。
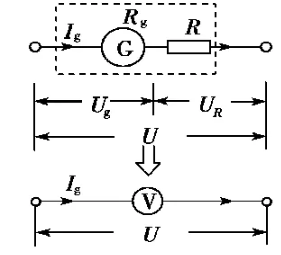
下面我们来算一下,总电压U与表头电压Ug的关系:
U=Ug+UR=Ug+IgR=Ug+UgR/Rg=(1+R/Rg)Ug
也就是说在表头上串联一个电阻R就可以扩大(1+R/Rg)倍的量程,那么,如果我们想要扩大n倍量程,自然有n=1+R/Rg,很容易得到R=(n-1)Rg。也就是说,如果我想将表头改装成n倍量程的电压表,就需要在表头上串联一个阻值R=(n-1)Rg的电阻。
我们可以很容易算出改装后电压表的总电阻为nRg,我们以一个Ig=100μA,Rg=1000Ω,Ug=0.1V的表头为例,将其改装成3V量程的电压表,改装后的电压表总电阻为30kΩ,这就是为啥初中将电压表看成断路的原因,电阻太大了。
当然,上面只是对电路进行改造,我们还需要重新绘制表盘,我们需要将表盘上每个位置的电流值I换成U。以上面的表头为例,100μA刻度要改成3V,50μA刻度要改成1.5V,以此类推。最后封装好就可以出厂了。
大家对实验室的电压表应该很熟悉,实验室的电压表通常有两个量程,那么其内部的结构应该是怎么样的呢?其实很简单,我们在表头上串联两个电阻就可以了。如下:
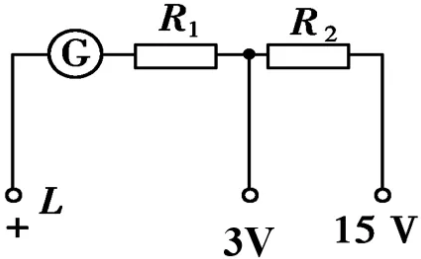
如果表头还是我们刚才假设的参数,根据上面的分析,我们很容易得到R1=2.9kΩ,R2=12kΩ。电表改装后当然还需要进行校准,由于文章长度的原因关于校准部分,将在以后合适的时候推出。
改装成大量程电流表
表头的量程通常很小,如果需要测量较大的电流,就需要改装。同样的,如果表头能找到一个伙伴,让它的伙伴承担一部分电流,并且表头还能知道它的伙伴承担了多少电流,那就完成了这件事情。
要做到上面的事情,我们就想到并联分流,将一个已知电阻与表头并联,这个电阻就会分掉一部分电流,同时因为是并联关系,表头很容易知道它的伙伴身上的电流。具体如下:
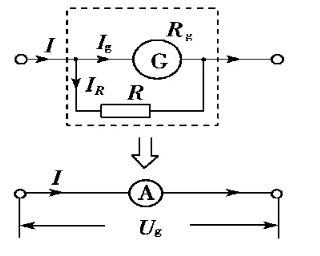
我们来算一下干路电流与流经表头电流的关系:
I=Ig+IR=Ig+IgRg/R =(1+Rg/R)Ig
也就是说在表头上并联一个电阻R就可以扩大(1+Rg/R)倍量程,那么如果我想扩大n倍量程,只需要保证(1+Rg/R)=n,也就是需要并联一个R=Rg/(n-1)的电阻就可以了。
同样的,我们很容易算出改装后的电流表的总电阻为Rg/n,我们以一个Ig=100μA,Rg=1000Ω,Ug=0.1V的表头为例,将其改装成0.6A量程的电流表,改装后的电流表总电阻为1/6Ω,这就是为啥初中将电流表看成导线的原因,电阻很小。
当然,上面只是对电路进行改造,我们还需要重新绘制表盘,我们需要将表盘上每个位置的电流值I换成nI。以上面的表头为例,100μA刻度要改成0.6A,50μA刻度要改成0.3A,以此类推。最后封装好就可以出厂了。
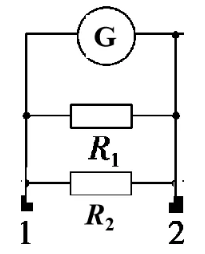
大家在实验室见到的电流表通常都是有两个量程的,那实验室的电流表内部结构应该是怎样的呢?好像就比电压表要复杂一些,如果直接并联两个电阻,如下图,这样只能实现一个量程,无法实现两个量程。
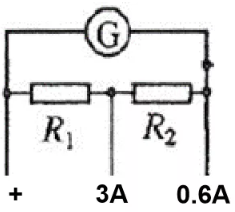
于是,人们就思考这样一个电路,如下图:当接0.6A接口时,R1+R2共同作为分流电阻,容易算出R1+R2=Rg/5999。当接3A接口时,就只有R1作为分流电阻了,但要特别注意,与R1并联的不再是Rg,而是Rg+R2,所以这个时候应该有R1=(Rg+R2)/29999。
可以求得上述R1和R2,我们可以发现这里算出来的电阻会比电压表改装时算出来的要复杂一些,通常也就会用约等处理。
同样的,由于文章长度原因,关于改装后电流表的校准将在后面合适的时候推出。
最后,我想强调一个思想,那就是电流表、电压表、电阻三者其实是一个东西,仔细体会这个思想,对后面的电学实验学习有极大的帮助:
电流表就是一个能读出流经自己的电流的特异功能电阻
电压表就是一个能读出自己身上的电压的特异功能电阻
电流表既是电流表,又是电压表,还是电阻
电压表既是电压表,又是电流表,还是电阻
电阻不仅是电阻,还可以是电流表,也可以是电压表
高中物理知识点总结
外部进行改装比较麻烦,为什么不能从电表内部进行改装
这么好的干货居然没人,真是可惜了