高中物理力学之弹簧有关题型

对于弹簧有关题目，是同学们高中物理学习的过程中非常头疼的问题，因为一但涉及弹簧有关题型，往往是变力问题，需要分析力如何变化，加速度如何变化，很多同学往往很容易弄错，下面刘叔就弹簧有关题型汇总一下。

弹簧有关的加速度突变问题。

弹簧有关加速度问题，始终抓住弹簧上的力不能突变，而绳杆上的力可以突变。

例题1：如下图所示，质量为m1、m2的物块用弹簧连接在竖直平面上，m2放在一块木板上，整体保持静止，现将木块从底部瞬间抽出，问抽出的瞬间，m1、m1的加速度的大小。

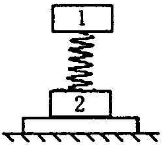
分析：在抽出之前，m1、m2处于平衡状态，所受合力为零，m1受到竖直向下的重力和竖直向上的弹力处于平衡状态，m2受到木板竖直向上的支持力和重力以及弹簧的弹力处于平衡状态。当将木板瞬间抽出时，木板对m2的支持力瞬间消失，但弹簧的弹力不变，所以m1受力情况不变，然处于平衡状态；但m2只有竖直向下的重力和竖直向下的弹力。

对m1受力分析可知：a1=0.

对m2受力分析可知：a2=（m2+m1）g/m2（方向竖直向下）。

例题2：如下图所示，小球A、B的质量分别为m1、m2，当剪短细绳的瞬间，求小球A、B的加速度大小。

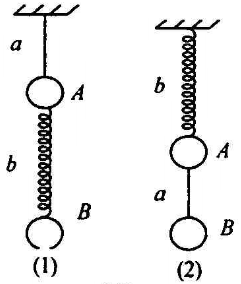
分析：对（1），当剪短细绳，A球将受到竖直向下的重力和竖直向下的弹力，两者的合力提供小球A的加速度，小球B将受到竖直向下的重力和竖直向上的弹力。对（2），剪短瞬间，小球A将受到自身的重力和弹簧向上的弹力，小球B将仅受到自身的中。

对（1）中小球A：a1=（m1+m2）g/m1（方向竖直向下）。

对（1）中小球B：a2=0。

对（2）中小球A：a1=m2g/m1（方向竖直向上）。

对（2）中小球B：a2=g（方向竖直向下）。

多弹簧连接有关劲度系数变化问题

1、两根弹簧串联连接后劲度系数的变化关系。

如下图所示：劲度系数分别为ka、kb的弹簧串联连接，问串联以后弹簧的劲度系数为多少？

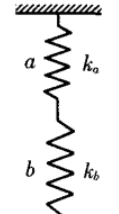
分析：设弹簧受到向下的拉力F作用，a弹簧伸长量La=F/ka，b弹簧伸长量Lb=F/kb，弹簧总伸长量L=La+Lb。所以a、b两弹簧串联以后的劲度系数k=F/(La+Lb）=1/(1/ka+1/kb)。

2、两根弹簧并联连接后劲度系数的变化关系。

如下图所示：弹簧A、b弹簧的劲度系数分别为ka、kb，两者并联连接，问并联以后弹簧的劲度系数为多少？

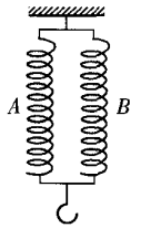
分析：设A、B弹簧伸长L，则弹簧所受的拉力F=kaL+kbL，并联以后的劲度系数k=F/L=ka+kb。

总结：两根以上的弹簧串联、并联后的劲度系数也是一样，和电阻的串并刚好相反。

串联后弹簧的劲度系数的倒数等于各个弹簧劲度系数的倒数和。

并联后弹簧的劲度系数等于各个弹簧的劲度系数之和。

弹簧有关的加速度变化问题

如下图所示，弹簧开始处于原长，在弹簧的正上方A点静止释放一物块，物块在B点与弹簧接触，运动的最低点为C点，求物块在A到C的过程中加速的变化情况。

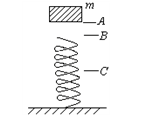
分析：对物块整个过程受力分析，A到B过程只受重力作用，所以在此过程物块做自由落体运动，加速度不变；B到C的过程中，物块受到重力和向上的弹簧弹力作用，这两个力的合力提供物块的加速度，那么物块在B到C的过程中会一直做减速运动吗？肯定不会，因为在物块在压缩弹簧的开始阶段，重力会比弹力要大，此阶段物块还是向下做加速度运动，但此阶段过程中弹力会增大，所以重力与弹力的合力会减小，即加速度会减小，直到弹力等于重力，当弹力等于重力时，加速度为零，速度达到最大，物块会继续向下运动，一但向下运动，弹簧继续被压缩，弹力会大于重力，合外力向上，物块会做减速运动，物块越往下运动，合外力就越大，物块向上的加速度就越大，直到物块速度减为零，即达到C点。

物块从A到C点的加速度变化情况：A到B加速不变；B到C过程中，加速度先减小和增大。

物块从A到C点的速度变化情况：A到B做匀加速运动；B到C过程中，速度先增大后减小。

高中物理知识点总结

高中物理视频大全

发表回复