
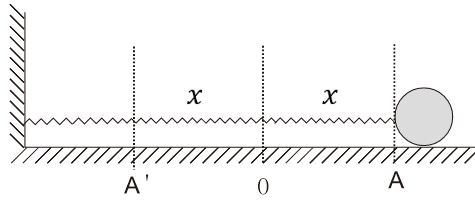
物体所受的力与它偏离平衡位置的位移大小成正比(F=-kx),并且总指向平衡位置,则物体所做的运动叫做简谐运动。如下图所示,O点为弹簧原长端点,水平面光滑,质量为m的小球在弹簧弹力的作用下在A^′和A之间做往复运动,在此运动中,小球受的力与它偏离平衡位置(O点)的位移大小成正比,并且总指向平衡位置,小球运动形式为简谐运动。
如果从平衡位置开始计时,则简谐运动的振动方程x=A\sin ωt ,周期T=2\pi \sqrt{\cfrac{m}{k}} ,下面刘叔物理用几种方法推出简谐运动的振动方程。
1、匀速圆周运动投影法
先说结论:匀速圆周运动在任意直径方向的投影是简谐振动

匀速圆周运动在任意直径方向的投影是简谐振动
如下图所示,我们讨论一下匀速圆周运动在x轴上的投影规律。已知物体作匀速圆周运动的初始位置在x轴,角速度为ω,半径为r。
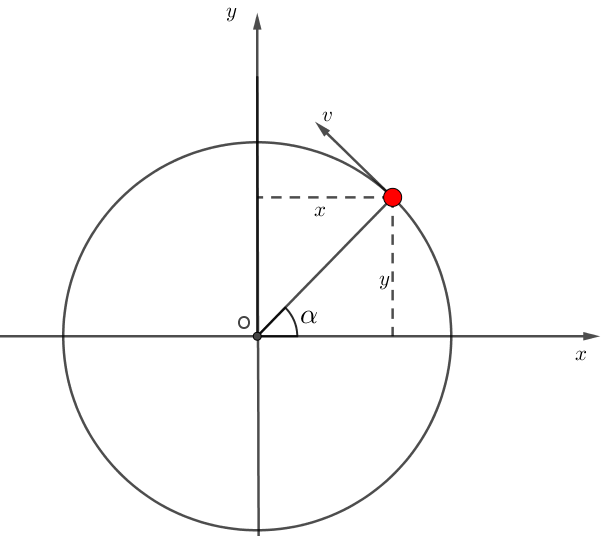
运动轨迹在x轴上的投影为:x=rcosα=rcos(wt)
线速度在x轴上的投影为:v=ωrsin(wt)
加速度在x轴上的投影为:a=-ω^2rcos(wt)
由加速度公式:a=-ω^2rcos(wt),我们可以知道F=ma=-mω^2rcos(wt),再将x=rcos(wt)代入。
可得:F=-mω^2x,令k=mω^2
最后得到:\red {F=-kx}
再由k=mω^2,得到ω=\sqrt{\cfrac{k}{m}},由周期公式T=\cfrac{2π}{ω},代入可得,T=2\pi \sqrt{\cfrac{m}{k}} ,即简谐振动周期公式。
2、费曼推理法
由{F=-kx⇒m\cfrac{d^2x}{dt^2}=-kx⇒\cfrac{d^2x}{dt^2}=-\cfrac{k}{m}x}
令\cfrac{k}{m}=1,得:\cfrac{d^2x}{dt^2}=-x
从上面可知,一个函数对时间两次求导后,居然变回了自己得相反数,可以发现,正余弦函数都可以满足,先不妨设置x=cos (t)
时间t的单位是秒,但余弦cos括号里的单位应该是以度为单位的,所以括号里的不应该只有时间,应该还有一个量,让它与时间相乘等于角度量,很容易得出这个量是角速度ω,这样振动方程就是下面这个样子:
x=cos (ωt)
为了知道ω是什么,将上式代入\cfrac{d^2x}{dt^2}=-x,可得:
\cfrac{d^2x}{dt^2}=-ω^2x
通过比较发现,当令ω^2=\cfrac{k}{m}时,就与{\cfrac{d^2x}{dt^2}=-\cfrac{k}{m}x}完全一样了。ω=\sqrt{\cfrac{k}{m}}
对函数x=cos (ωt)分析:
(1)很明显是个周期函数,周期T=\cfrac{2π}{ω}=\cfrac{2π}{\sqrt{\cfrac{k}{m}}}=2π\sqrt{\cfrac{m}{k}},简谐振动也是一个周期性的振动,这一点满足。
(2)当t=0时,x=1,为函数的最大值,这说明当t=0时,在简谐振动的最大位置,即从简谐振动的最大位移开始振动,但这里有一个问题,最大位置的位移不一定是个1,所以这里我们需要配一个常数,表示简谐振动的最大位移,这里我们用A表示,这样函数公式就变成x=Acos (ωt)。
(3)如果不是从简谐振动的最大位移开始振动,而是从平衡位置开始振动,则需要当t=0时,x=0,就相当于x=A\cos ω(t+t_0),此时的ωt_0=\cfrac{π}{2},可以理解到,ωt_0决定振动的初始位置,我们将这个位置取个专业一点的名字,叫做初相,用φ表示,到此,我们得出的振动的方程为:
x=Acos (ωt+φ)
上面这个方程很明显就是简谐运动方程。
3、能量守恒法
小球在做简谐运动的过程中弹簧和小球组成的系统能量守恒,在最大振幅A时,系统的能量E=\cfrac{1}{2}kA^2为一定值。
由能量守恒:\cfrac{1}{2}kA^2=\cfrac{1}{2}m(\cfrac{dx}{dt})^2+ \cfrac{1}{2}kx^2
化简可得:(\cfrac{dx}{dt})^2=\cfrac{k}{m} (A^2-x^2)
\cfrac{dx}{dt}=ω\sqrt{ A^2-x^2} 其中ω^2=\cfrac{k}{m}
分离变量:\cfrac{dx}{\sqrt{ A^2-x^2}}=ωdt
两边积分:\int{\cfrac{dx}{\sqrt{ A^2-x^2}}}=ω\int{dt}
可得:arcsin(\cfrac{x}{A})=ωt+C
最后得:\red {x=Asin(ωt+C)}
(1)如果从平衡位置开始计时,t=0时,x=0,C=0
振动方程x=A\sin ωt
(2)如果从最大振幅位置开始计时,t=0时,x=A,C=\cfrac{π}{2}
振动方程x=A\sin (ωt+\cfrac{π}{2}) =Acos ωt
4、积分法
简谐运动满足F=-kx⇒ma=-kx
又由a=\cfrac{dv}{dt}=\cfrac{dv}{dx}\cfrac{dx}{dt}=\cfrac{dv}{dx}v
可得:m\cfrac{dv}{dx}v=-kx⇒mvdv=-kxdx
两边积分:m\int vdv=-k\int xdx
可得:\cfrac{1}{2}mv^2=-\cfrac{1}{2}kx^2+C⇒v^2=-\cfrac{k}{m}x^2+2C
令\cfrac{k}{m}=ω^2。当v=0时,x=A,C=\cfrac{ω^2A^2}{2},2C=ω^2A^2
由:v^2=-\cfrac{k}{m}x^2+2C⇒(\cfrac{dx}{dt})^2=-ω^2x^2+ω^2A^2
可得:\cfrac{dx}{dt} =\sqrt{-ω^2 x^2+ω^2 A^2}⇒\cfrac{dx}{\sqrt{ A^2-x^2}}=ωdt
两边积分:\int{\cfrac{dx}{\sqrt{ A^2-x^2}}}=ω\int{dt}
可得:arcsin(\cfrac{x}{A})=ωt+C
最后得:\red {x=Asin(ωt+C)}
(1)如果从平衡位置开始计时,t=0时,x=0,C=0
振动方程x=A\sin ωt
(2)如果从最大振幅位置开始计时,t=0时,x=A,C=\cfrac{π}{2}
振动方程x=A\sin (ωt+\cfrac{π}{2}) =Acos ωt
5、泰勒级数法
泰勒级数法相对就比较高级了,那什么是泰勒级数呢,通俗的说就是一个不常见的函数,我们用一些熟悉的幂函数不断去拟合这个函数,说到底就是用来近似的、仿造的。
泰勒级数展开式子:f(x)=f(0)+\cfrac{f^{(1)} (x)}{1} x+\cfrac{f^{(2)} (x)}{2!} x^2+\cfrac{f^{(3)} (x)}{3!} x^3+...+\cfrac{f^{(n)} (x)}{n!} x^n
设函数x(t)=x(0)+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5...+a_nt^n
对x(t)求一阶段导得:\cfrac{dx}{dt}=a_1+2a_2t+3a_3t^2+4a_4t^3+5a_4t^4...+na_nt^{(n-1)}
对x(t)求二阶段导得:\cfrac{d^2x}{dt^2}=2a_2+6a_3t+12a_4t^2+20a_4t^3+...+n(n-1)a_nt^{(n-2)}
凑成简谐振动式子:\cfrac{d^2x}{dt^2}+ω^2x=(2a_2+ω^2x(0))+(6a_3+ω^2a_1)t+(12a_4+ω^2a_2)t^2+(20a_5+ω^2a_3)t^3+...=0
需要保证上式对任意t,等于零恒成立,则上式各项系数为零。
即:2a_2+ω^2x(0)=0,6a_3+ω^2a_1=0,12a_4+ω^2a_2=0,20a_5+ω^2a_3=0,…
可得:a_1=0,a_2=-\cfrac{1}{2!}ω^2x(0),a_3=0,a_4=\cfrac{1}{4!}ω^4x(0),a_5=0,a_6=-\cfrac{1}{6!}ω^6x(0),…
可得:x(t)=x(0)+a_2t^2+a_4t^4+...⇒x(t)=x(0)-\cfrac{1}{2!}(ωt)^2x(0)+\cfrac{1}{4!}(ωt)^4x(0)+...=x(0)[1-\cfrac{1}{2!}(ωt)^2+\cfrac{1}{4!}(ωt)^4+...]
由于函数cos (ωt)的泰勒级数展开cos (ωt)=1-\cfrac{1}{2!}(ωt)^2+\cfrac{1}{4!}(ωt)^4+...
最后可得:\red {x(t)=x(0)cos (ωt)},即简谐运动振动方程。
高中物理知识点总结
One comment
Comments are closed.