
一、问题讨论
如下图所示,中心天体在O点,1为椭圆轨道,2为圆形轨道,两轨道相切A点,那么椭圆轨道和圆轨道相切位置A点的向心加速度是否相等呢?
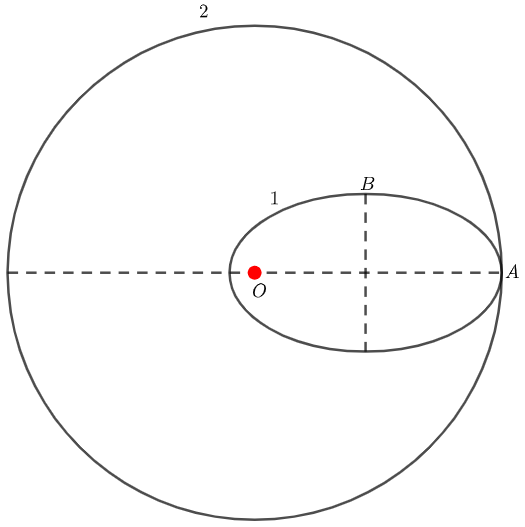
讨论分析:将这个问题拿出来分析的原因是看到一些参考书和课件,说在A点,圆轨道的向心加速度大于椭圆轨道的向心加速度,因为圆轨道A点速率大于椭圆轨道A的速率,根据a_向=\cfrac{v^2}{r},可知圆轨道的向心加速度大,刘叔物理认为这样分析明显有个错误,就是把椭圆轨道在A点的曲率半径等于圆轨道的半径,椭圆轨道在A点的曲率半径是明显小于圆轨道半径的,其实通过证明,可以得到椭圆轨道在A点的曲率半径\rho_A=\cfrac{b^2}{a}(a为长半轴,b为短半轴),那么椭圆轨道和圆轨道在A点的向心加速度大小是怎么样的呢?其实是相等的。
不管是圆轨道还是椭圆轨道,在A点速度方向均与万有引力方向垂直,万有引力全部提供向心力,产生向心加速度,所以向心加速度相等。
二、求椭圆轨道短轴端点和长轴端点处的曲率半径
设离中心天体无穷远处引力势能为零,则离中心天体距离为d时引力势能E_p=-\cfrac{GMm}{d},如下图所示,A点距离中心天体距离为a+c,B点距离中心天体距离为a。

在A、B两点由能量守恒可得:
-\cfrac{GMm}{a+c}+\cfrac{1}{2}m{v_A}^2=-\cfrac{GMm}{a}+\cfrac{1}{2}m{v_B}^2
在A、B两点根据开普勒第二定律:v_Ba\cos \theta =v_A(a+c)
在A点:G\cfrac{Mm}{{(a+c)}^2}=m\cfrac{{v_A}^2}{\rho_A}
在B点:G\cfrac{Mm}{a^2}\cos\theta=m\cfrac{{v_B}^2}{\rho_B}
其中\cos \theta=\cfrac{b}{a}
椭圆满足a^2=b^2+c^2
联立以上各式可得:\rho_A=\cfrac{b^2}{a},\rho_B=\cfrac{a^2}{b}
三、万有引力与航天一些结论
1、质量分布均匀的薄球壳在其内部产生的引力场场强处处为零。(或者说球壳对内部物体的引力为零)。推广:均匀椭球体外壳对其空腔中任意一点的引力大小也为零。
2、在半径为R的均匀球体内部挖去半径为r的一个小球(两球圆心不重合),空腔内部的引力场恒定不变,物体在空腔内的加速度恒定。
3、质量为m物体,可视为质点,从无限远处靠近质量为M的均匀星球,设星球的半径为R,物体与星球M圆心的距离为r,则引力产生的加速度a与r满足如下关系:
(1)当r\geq R时,a=\cfrac{GM}{r^2}
(2)当r<R 时,a=\cfrac{4}{3}G\rho \pi r
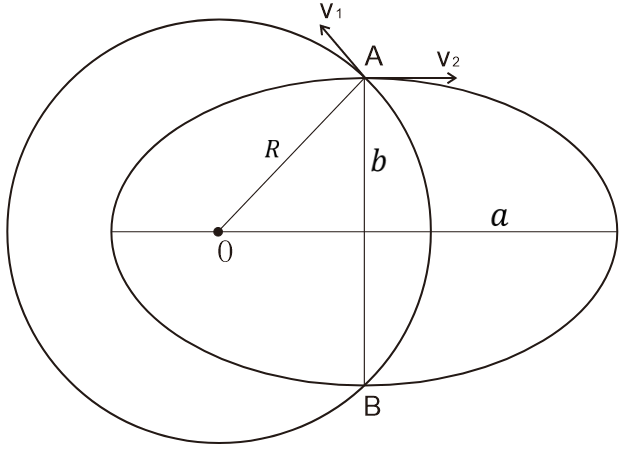
4、两星球环绕同一中心天体运动,一个圆形轨道,一个椭圆轨道,如果周期相同,则它们轨道交点处的速率相等,如下图,中心天体在O点,v_1=v_2
高中物理知识点总结