
在圆周有关题目中,经常会出现两物块在圆盘上通过绳关联随着圆盘一起做圆周运动的题目,这类题目运动过程分析相对比较繁琐,是圆周运动相对较难的题目,本篇文章刘叔物理对这类的题目分析总结一下。
先说结论:
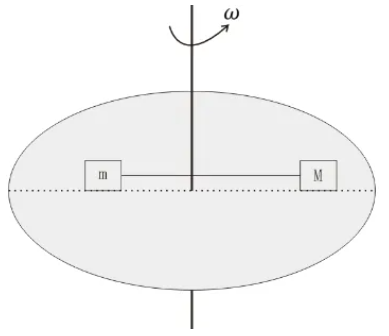
如下图,质量为m和M的两物块用轻绳相连,放在以角速度转动的粗糙圆盘上,当圆盘角速度增大到一定值时,m和M会相对圆盘滑动,根据系统牛顿第二定律,滑动的方向一定是朝着以m、M为系统的质心一侧滑动,如果质心在转轴上,则不会滑动(除非轻绳断)。
例题1:
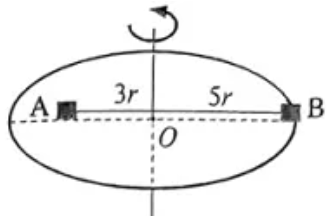
如图,半径为5r的水平圆形转盘可绕竖直轴转动,圆盘上放有质量均为m的小物体A、B。A、B到转盘中心O的距离分别为3r、5r,A、B间用一轻质细线相连,圆盘静止时,细线刚好伸直无拉力。已知A与圆盘间的动摩擦因数为μ,B与圆盘间的动摩擦因数为2μ。设最大静摩擦力等于滑动摩擦力,重力加速度为g,A、B均可视为质点,现让圆盘从静止开始逐渐缓慢加速,分析A、B物体在圆盘上运动的整个过程。
详细解析如下:
由于A、B物块质心在右侧(B一侧),根据系统牛顿第二定律,A、B最终一定向B物块一侧滑动。通过分析可知,当圆盘角速度\omega=\sqrt{\frac{μg}{3r}}时,绳子恰好没有张力,根据角速度的不同,分以下几种情况讨论:
(1)当0<\omega≤\sqrt{\frac{μg}{3r}}时
对A:f_A=3mω^2 r
对B:f_B=5mω^2 r
此过程中绳上的张力为零,物块A所需要的向心力由圆盘对其指向圆心的摩擦力提供,物块B所需要的向心力由圆盘对其指向圆心的摩擦力提供;当\omega=\sqrt{\frac{μg}{3r}}时,f_A达到最大值,f_B未达到最大值。
(2)当\sqrt{\frac{μg}{3r}}<\omega≤\sqrt{\frac{μg}{2r}}时
对A:T+μmg=3mω^2 r
对B:T+f_B=5mω^2 r
此过程中绳上的张力不断增大;f_B指向圆心不断增大,\omega=\sqrt{\frac{μg}{2r}}时,f_B=2μmg达到最大;f_A=μmg指向圆心保持不变。
(3)当\sqrt{\frac{μg}{2r}}<\omega≤\sqrt{\frac{μg}{r}}时
对A:T+f_A=3mω^2 r
对B:T+2μmg=5mω^2 r
此过程中绳上的张力不断增大;f_B=2μmg指向圆心保持不变;f_A指向圆心慢慢减小,当\omega=\sqrt{\frac{μg}{r}}时,f_A=0
(4)当\sqrt{\frac{μg}{r}}<\omega≤\sqrt{\frac{3μg}{2r}}时
对A:T-f_A=3mω^2 r
对B:T+2μmg=5mω^2 r
此过程中绳上的张力不断增大;f_B=2μmg指向圆心保持不变;f_A 指向背离圆心慢慢增大,当\omega=\sqrt{\frac{3μg}{2r}}时,f_A=μmg
(5)当\omega>\sqrt{\frac{3μg}{2r}}时
A、B两物块相对圆盘滑动
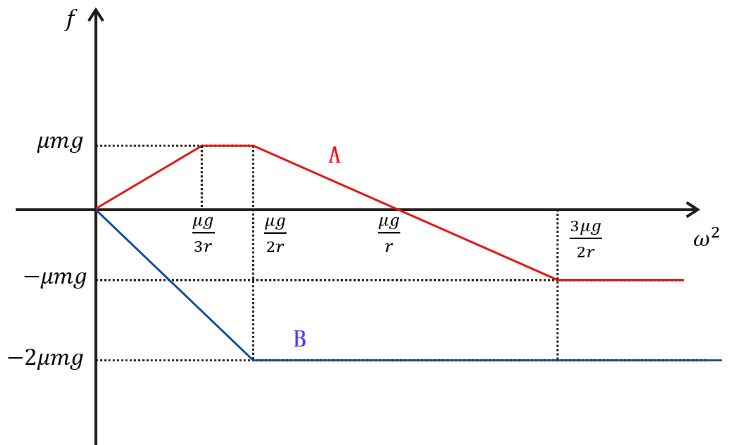
规定向右为正,两物块所受摩擦力与角速度平方图像如下图所示
例题2:
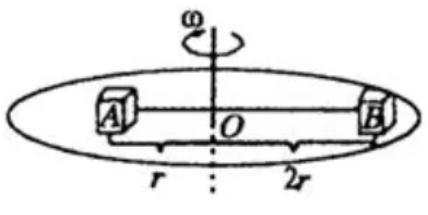
如图所示,在匀速转动的水平盘上,沿半径方向放着用细线相连的质量相等的两个物体A和B,它们分居圆心两侧,与圆心距离分别为RA=r,RB=2r,与盘间的动摩擦因数μ相同,当圆盘转速加快到两物体刚好还未发生滑动时,最大静摩擦力等于滑动摩擦力,分析A、B物体在圆盘上运动的整个过程。
详细解析如下:
由于A、B物块质心在右侧(B一侧),根据系统牛顿第二定律,A、B最终一定向B物块一侧滑动。通过分析可知,当圆盘角速度\omega=\sqrt{\frac{μg}{2r}}时,绳子恰好没有张力,根据角速度的不同,分以下几种情况讨论:
(1)当0<\omega≤\sqrt{\frac{μg}{2r}}时
对A:f_A=mω^2r
对B:f_B=2mω^2r
此过程中绳上的张力为零,物块A所需要的向心力由圆盘对其指向圆心的摩擦力提供,物块B所需要的向心力由圆盘对其指向圆心的摩擦力提供;当\omega=\sqrt{\frac{μg}{2r}}时,f_B达到最大值,f_A未达到最大值。
(2)当\sqrt{\frac{μg}{2r}}<\omega≤\sqrt{\frac{μg}{r}}时
对A:T+f_A=mω^2r
对B:T+μmg=2mω^2r
此过程中绳上的张力不断增大;f_A指向圆心,大小从\frac{μmg}{2}不断减小到零,当\omega=\sqrt{\frac{μg}{r}} 时,f_A=0;f_B=μmg指向圆心保持不变。
(3)当\sqrt{\frac{μg}{r}}<\omega≤\sqrt{\frac{2μg}{r}}时
对A:T-f_A=mω^2r
对B:T+μmg=2mω^2r
此过程中绳上的张力不断增大;f_A指向背离圆心,大小从零不断增大到μmg,当\omega=\sqrt{\frac{2μg}{r}}时,f_A=μmg;f_B=μmg指向圆心保持不变。
(4)当\omega>\sqrt{\frac{2μg}{r}}时
A、B两物块相对圆盘滑动
规定向右为正,两物块所受摩擦力与角速度平方图像如下图所示

高中物理知识点总结