
极值问题,是考试中经常出现的一类,极值的出现往往伴有相同的条件,运动学中出现极值往往速度相等,力学中出现极值往往合力为零,电学中出现极值往往是功率最大或者最小,带电粒子在磁场中出现极值往往速度相切、圆心角最大或最小等等,但还有一类的极值比较隐含,就是“三分之二”引起的极值问题,这类问题往往对学生的理解归纳能力、数学计算能力有较高的要求。
本文分别从高中物理几个不同的知识点例题入手,举例说明“神奇三分之二”的存在。
例题1 竖直平面内有一个四分之一圆弧AB,OA为水平半径,现从圆心O处以不同的初速度水平抛出许多个相同质量的小球,小球可以看作质点,不计空气阻力,小球落到圆弧上时最小的速度为多少?
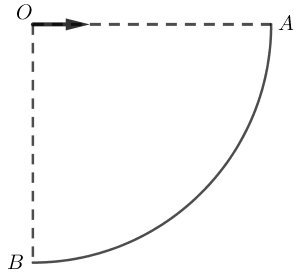
解析:定性的分析,小球平抛的初速度越小,小球落点离B点越近,重力做功越大;小球平抛的初速度越大,小球落点离B点越远,重力做功越小。很明显通过定性的分析判断不了落在哪个位置动能小,但可以隐约察觉到在A和B之间弧上的某一点上,需要做定量计算。
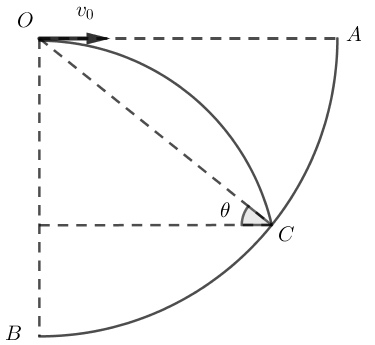
如上图所示,设四分之一圆的半径为R,小球抛出的初速度为Vo,小球落在圆上的速度为V
竖直方向:![]() 水平方向:
水平方向:![]()
联立上面两式可得:![]()
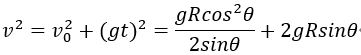
![]()
当且仅当![]() ,等号成立,可得
,等号成立,可得![]()
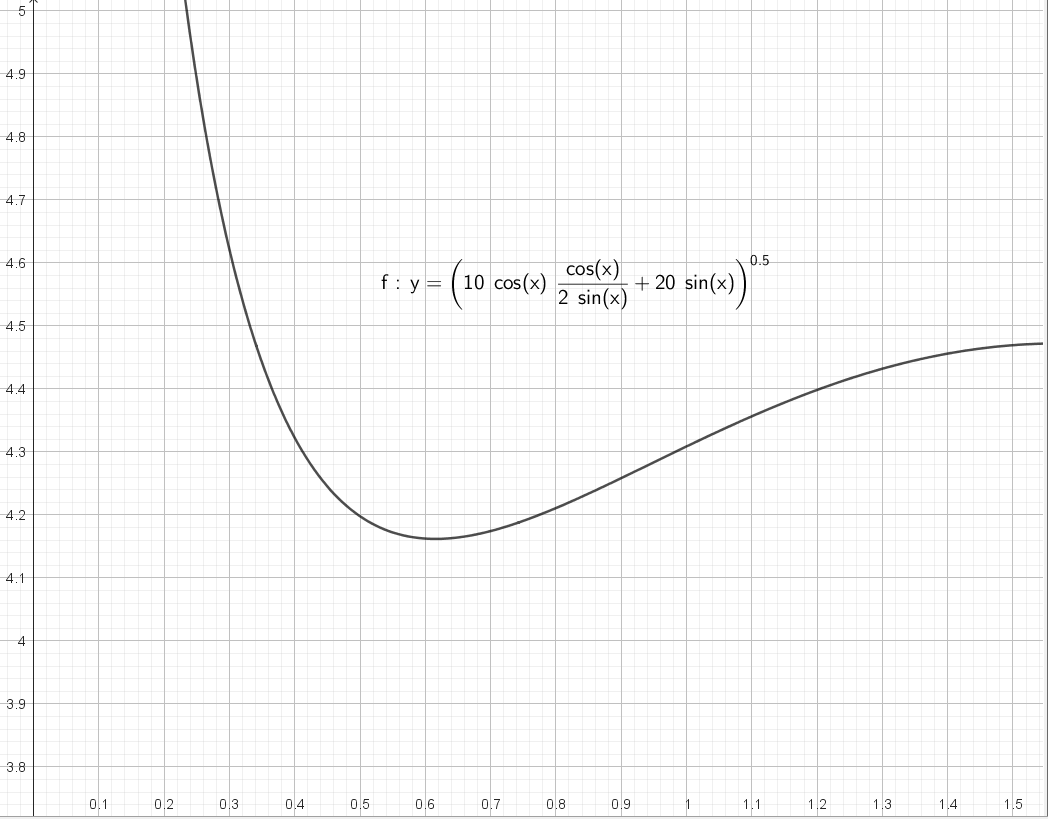
当gR=10时,通过GeoGebra模拟速度与θ的变化如下图所示
例题2 光滑的半圆弧面固定在水平面上,一可以看成质点的物块从半圆弧面顶端静止滑下,问物块下滑的过程中,物块何时脱离半圆弧面?
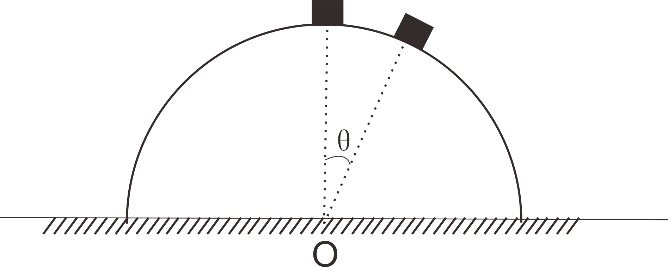
解析:滑块脱离弧面时,滑块与弧面间的作用力为零,此时滑块做圆周运动的向心力恰好由其重力沿着弧面半径方向的分量提供,大小为mgcosθ
整个过程中对滑块由动能定理:![]()
由![]() ,可得
,可得![]()
解得 cosθ=2/3
例题3 如下图所示,光滑的墙角竖直放置着一根长为L的轻杆,轻杆两端固定着两个质量为m的A、B小球,现B球受到轻微扰动向右运动,问A球何时脱离墙面?
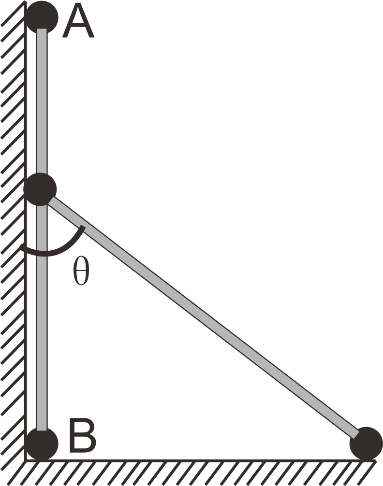
解析:设球A与墙面恰好分离时球A的速度为![]() ,球B的速度为
,球B的速度为![]()
两球沿着轻杆的速度相等:![]()
对整个过程机械能守恒:![]()
脱离时,球B速度最大![]()
![]()
经过整理可得:![]()
由![]()
当且仅当cosθ=cosθ=2—2cosθ取等号,可得![]()
例题4 如下图所示,长度为L轻细线一端固定于O点,一端系一质量为m的小球,水平拉直细线,在竖直面内将小球静止自由释放,问何时重力功率最大?
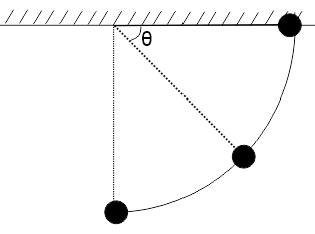
解析:如上图所示,当细线与水平方向成θ时
对小球:![]()
联立得:![]()
令![]() ,对X求导可得
,对X求导可得![]()
当![]() 时,f(x)有最大值,即
时,f(x)有最大值,即![]() 时,功率P有最大值。
时,功率P有最大值。
例题5 在同种点电荷形成的电场中,点电荷中垂线上的电场强度何时最大?
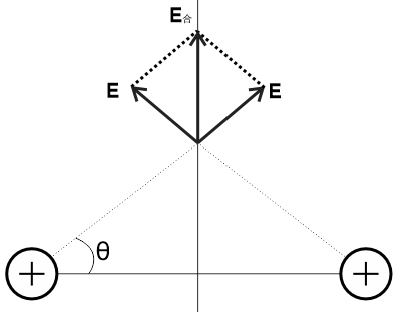
解析:设两点电荷之间的距离为2L,中垂线点与点电荷的连线和水平方向成θ。
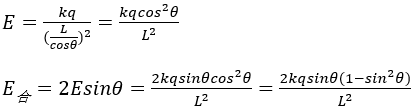
令![]() ,对X求导可得
,对X求导可得![]()
当![]() 时,f(x)有最大值,即
时,f(x)有最大值,即![]() 时,电场强度最大。
时,电场强度最大。
例题6 如下图所示,竖直的半圆弧局域中存在垂直纸面的磁场,一根金属杆从半圆弧上端水平自由下落,问何时金属杆产生的电动势最大?
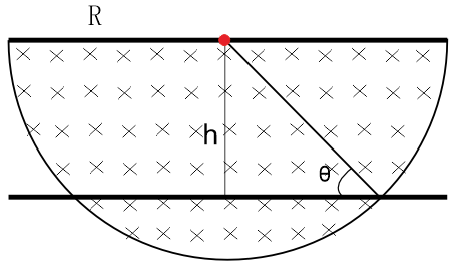
解析:杆做自由落体运动,下降h时的速度![]()
此时切割的长度 L=2Rcosθ
金属杆产生的电动势![]()
![]()
令![]() ,对X求导可得
,对X求导可得![]()
当![]() 时,f(x)有最大值,即
时,f(x)有最大值,即![]() 时,金属杆产生的电动势最大。
时,金属杆产生的电动势最大。
高中物理知识点总结