行星与太阳间的引力
1.推导过程
如图所示，设行星的质量为m，速度为v，行星与太阳间的距离为r，则行星绕太阳做匀速圆周运动的向心力为F=mν²/r①
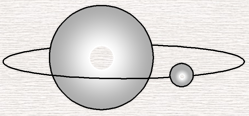
天文观测可以测得行星公转的周期T，并据此可求出行星的速度v＝2πr/T②
联立①②整理后得F＝4π²mr/T²③
根据开普勒第三定律得r³/T²＝k④
联立③④得F＝4π²mk/r²
上式除m、r以外，其余都是常量，所以F∝m/r²
力的作用是相互的，行星与太阳的引力也应与太阳的质量m太成正比，即F∝m太/r²。
2.表达式：
（式中量G与太阳、行星都没有关系。太阳与行星间引力的方向沿着二者的连线。）
月—地检验
1.假设
(1)假设地球与月球间的作用力和太阳与行星间的作用力是同一种力，它们的表达式也应该满足F＝Gm地m月/r²。根据牛顿第二定律，月球绕地球做圆周运动的向心加速度a月＝F/m月＝Gm地/r²
(2)假设地球对苹果的吸引力也是同一种力，同理可知，苹果的自由落体加速度a苹＝F/m苹＝Gm地/R²。
上述公式中m地为地球质量，m月为月球质量，r为地球中心与月球中心的距离，R是地球中心与苹果间的距离。由以上两式可得a月/a苹＝R²/r²。由于月球与地球中心的距离r约为地球半径R的60倍，所以＝1/60²。
2.结论：月球绕地球运动的向心加速度与我们的预期符合得很好。这表明：地面物体所受地球的引力、月球所受地球的引力，与太阳、行星间的引力遵从相同的规律。
万有引力定律
1.内容：自然界中任何两个物体都相互吸引，引力的方向在它们的连线上，引力的大小与物体的质量m1和m2的乘积成正比，与它们之间距离r的二次方成反比。
2.表达式：F＝Gm1m2/r²。比例系数G叫作引力常量，适用于任何两个物体。
引力常量
1.引力常量的测定
英国物理学家卡文迪什在实验室里通过扭秤装置，比较准确地得出了G值，通常取G＝6.67×10-11N·m2/kg2。
2.引力常量测定的意义
(1)卡文迪什利用扭秤装置通过改变小球的质量和距离，证实了万有引力的存在及万有引力定律的正确性。
(2)引力常量的普适性成了万有引力定律正确性的有力证据。
对万有引力定律表达式F＝Gm1m2/r²的说明
(1)引力常量G：G＝6.67×10－11 N·m2/kg2；其物理意义为：引力常量在数值上等于两个质量都是1 kg的质点相距1 m时的相互吸引力。
(2)距离r：公式中的r是两个质点间的距离，对于质量均匀分布的球体，就是两球心间的距离。
(3)万有引力定律公式适用于计算质点间的相互作用，当两个物体间的距离比物体本身的尺度大得多时，可用此公式近似计算两物体间的万有引力。
(4)质量分布均匀的球体间的相互作用，可用此公式计算，式中r是两个球体球心间的距离。
(5)一个均匀球体与球外一个质点间的万有引力也可用此公式计算，式中的r是球体球心到质点的距离。
高中物理知识点总结
One comment