共点力
1．定义：如果一个物体受到两个或更多个力的作用，这些力共同作用在同一点上，或者虽不作用在同一点上，但它们的延长线交于一点，这样的一组力叫作共点力。
2．力的合成平行四边形定则只适用于共点力。
共点力平衡的条件
1．平衡状态：物体保持静止或匀速直线运动状态。
2．平衡条件：合力为0。
平衡条件的推论
(1)二力平衡：若物体在两个力作用下处于平衡状态，则这两个力一定等大、反向。
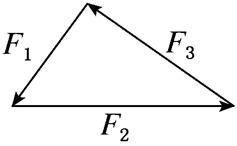
(2)三力平衡：若物体在三个共点力作用下处于平衡状态，则任意两个力的合力与第三个力等大、反向⇒表示三个力的有向线段首尾相接一定组成闭合的三角形，如图所示。
(3)多力平衡：若物体在n个共点力作用下处于平衡状态，则其中任意一个力必定与另外(n－1)个力的合力等大、反向。
（4）注意一点：物体静止时不一定处于平衡状态，一定要保持静止！（或者说处于静止状态），竖直上抛运动到最高的物体速度为零，物体瞬时静止，但不是平衡状态。
解答共点力平衡问题的三种常用方法
(1)合成法：物体在三个共点力作用下处于平衡时，将其中的任意两个力合成，其合力一定与第三个力平衡，从而把三力平衡问题转化为二力平衡问题。
(2)分解法：物体在三个共点力作用下处于平衡时，将其中任意一个力沿其他两个力的反方向分解，则每个方向上的一对力大小相等，方向相反，从而把三力平衡问题转化为两个方向上的二力平衡问题。
(3)正交分解法：物体在三个或三个以上的共点力作用下处于平衡时，将物体所受的各个力均向两个互相垂直的方向上分解，然后分别在这两个方向上列平衡方程。此时平衡条件可表示为：Fx合＝0，Fy合＝0。
解答共点力平衡问题的一般步骤
(1)选取研究对象，对于有相互作用的两个或两个以上的物体构成的系统，应明确所选研究对象是系统整体还是系统中的某一个物体(整体法或隔离法)。
(2)对所选研究对象进行受力分析，并画出受力示意图。
(3)对研究对象所受的力进行处理。对三力平衡问题，一般根据平衡条件画出力合成的平行四边形。对四力或四力以上的平衡问题，一般建立合适的直角坐标系，对各力按坐标轴进行分解。
(4)建立平衡方程。对于四力或四力以上的平衡问题，用正交分解法列出方程组。
1．“活结”与“死结”模型
(1)“活结”：一般是由轻绳跨过光滑滑轮或者绳上挂一光滑挂钩而形成的。绳子虽然因“活结”而弯曲，但实际上是同一根绳，所以由“活结”分开的两段绳子上弹力的大小一定相等，两段绳子合力的方向一定沿这两段绳子夹角的角平分线。
(2)“死结”：两侧的绳因结而变成了两根独立的绳，因此由“死结”分开的两段绳子上的弹力不一定相等。
2．“活杆”与“死杆”模型
(1)“活杆”：即轻杆用转轴或铰链连接，当杆处于平衡状态时，杆所受到的弹力方向一定沿着杆，否则会引起杆的转动。如图甲所示，若C为转轴，则轻杆在缓慢转动中，弹力方向始终沿杆的方向。
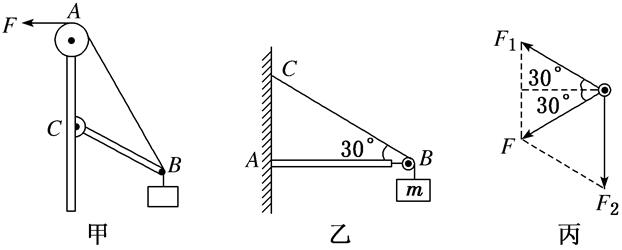
(2)“死杆”：若轻杆被固定不发生转动，则杆所受到的弹力方向不一定沿杆的方向。如图乙所示，水平横梁的一端A插在墙壁内，另一端装有一个小滑轮B，一轻绳的一端C固定于墙壁上，另一端跨过滑轮后悬挂重物m。滑轮对绳子的作用力应为图丙中两段绳中拉力F1和F2的合力F的反作用力，即死杆弹力的方向不沿杆的方向。
高中物理知识点总结
发表回复
要发表评论，您必须先登录。