
一、审题
要想迅速地理解题意,必须抓住题目中的关键词。比如是否考虑重力,在那个面内运动,粗糙还是光滑,有没有初速度,初速度向那个方向,直线运动还是曲线运动,是否匀变速运动,杆还是绳,弹簧与物体是否连接,弹簧是拉长还是压缩等;若有图像,要注意图像的横轴和纵轴,斜率和截距,图像的面积,图像的转折点等等。常见的临界词,如刚好,恰好,至多,至少等。特殊词语,如足够长,轻轻地,缓慢地,迅速地等。那些是已知条件,那些是所求的物理量。必要时画出草图帮助理解题意。
二,拆分物理过程
一个综合题,往往是由若干个子过程组合而成。对于这类题,我们可以“化整为零,各个击破”,即将整个过程拆分成几个子过程,然后对每个子过程运用规律列式求解,同时注意各个子过程之间的联系,比如时间的联系,速度的联系,位移的联系等。
【例1】(2019年4月浙江物理选考)某砂场为提高运输效率,研究砂粒下滑的高度与砂粒在传送带上运动的关系,建立如图所示的物理模型。竖直平面内有一倾角θ=37°的直轨道AB,其下方右侧放置一水平传送带,直轨道末端B与传送带间距可近似为零,但允许砂粒通过。转轮半R=0.4m、转轴间距L=2m的传送带以恒定的线速度逆时针转动,转轮最低点离地面的高度H=2.2m。现将一小物块放在距离传送带高h处静止释放,假设小物块从直轨道B端运动到达传送带上C点时,速度大小不变,方向变为水平向右。已知小物块与直轨道和传送带间的动摩擦因数均为μ=0.5。(sin37°=0.6)
(1)若h=2.4m,求小物块到达B端时速度的大小;
(2)若小物块落到传送带左侧地面,求h需要满足的条件;
(3)改变小物块释放的高度h,小物块从传送带的D点水平向右抛出,求小物块落地点到D点的水平距离x与h的关系式及h需要满足的条件。
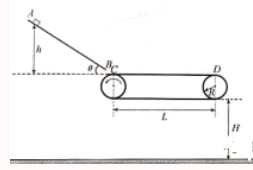
【分解】本题可拆分为4个过程,物体在斜面上下滑,物体在传送带上运动,物体刚到D点,物体离开D后做平抛运动。
【例2】(2016新课标II,35)如图,光滑冰面上静止放置一表面光滑的斜面体,斜面体右侧一蹲在滑板上的小孩和其前面的冰块均静止于冰面上.某时刻小孩将冰块以相对冰面3m/s的速度向斜面体推出,冰块平滑地滑上斜面体,在斜面体上上升的最大高度为h=0.3m(h小于斜面体的高度).已知小孩与滑板的总质量为m1=30kg,冰块的质量为m2=10kg,小孩与滑板始终无相对运动。
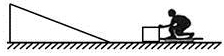
(ⅰ)求斜面体的质量;
(ⅱ)通过计算判断,冰块与斜面体分离后能否追上小孩?
【分解】本题可拆分为3个过程,小孩将冰块推出,冰块滑上斜面体,冰块与斜面体分离。
三,建立物理模型
将一个复杂的过程拆分成几个子过程后,对于每个子过程,我们要寻找它的特点,通过抽象,简化和类比的方法,将研究对象或研究过程转化为理想的物理模型。
【例1中的模型】对于例1中的4个过程,可以分别建立为以下的模型:
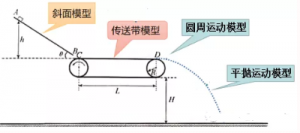
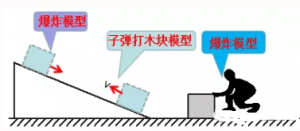
【例2中的模型】对于例2中的3个过程,可以分别建立为以下的模型:
四,确定解题方法
对于每个子过程,一般可以从以下三个角度考虑:
(1)动力学角度:用牛顿运动定律和运动学公式解题.
(2)能量角度:用动能定理、机械能守恒定律,功能关系,能量守恒定律解题.
(3)动量角度:用动量定理、动量守恒定律解题
三条途径的选用原则:
(1)当物体受到恒力作用做直线运动,而且又涉及时间和加速度时,一般从动力学角度考虑.
(2)当涉及功、能和位移时,一般从能量的角度考虑
对于单个物体,一般用动能定理,功能关系,或机械能守恒;
对于多个物体,或涉及弹簧,涉及相对位移时,一般用功能关系或能量守恒定律。
(3)当涉及多个物体或时间时,一般从动量的角度考虑,用动量定理、动量守恒定律解题.
【例1】在斜面上运动时,是个斜面模型,实质上是个匀变速直线运动模型,由于高度和倾角知道,可以求得加速度和位移,所以可以从动力学角度或能量角度解题;由于题中没给时间也不要求求时间,所以不从动量角度解题。
在传送带上运动时,是个传送带模型,对于传送带模型要特别留意物体与传送带能否共速,因为共速时,摩擦力会突变,加速度就会突变,运动性质也突变了。
刚好能从D点水平抛出时,在D点是个竖直面内的圆周运动模型,关键是找对向心力。
从D点抛出的过程是个平抛运动模型,由于竖直位移知道,所以采用分解位移的方法求解。
【例2】小孩将冰块推出的过程,相当于一个物体(刚开始小孩和冰块都静止)变成二个物体(冰块向左运动,小孩向右运动),是个爆炸模型,从动量和能量角度考虑。
冰块滑到斜面体最高点的过程,相当于二个物体变成一个物体,是个子弹打木块模型,从动量和能量角度考虑。
冰块从斜面体最高点滑下直到与斜面体分离的过程,相当于一个物体变成二个物体,是个爆炸模型,从动量和能量角度考虑。
作者:李幼峰 (高中物理模型及解法)
高中物理知识点总结
发表回复
要发表评论,您必须先登录。