高中物理人船模型

人船模型是动量守恒定律一个非常经典的模型，场景如下：

两个原来静止的物体发生相互作用时，若所受外力的矢量和为零，则动量守恒，两物体在相互作用的过程中，任意时刻速度大小之比等于质量的反比，这类问题都归于“人船模型”问题。

人船模型的特点

1．两物体满足动量守恒定律，即mv1=Mv2。

2．运动特点：人动船东，人停船停，人快船快，人慢船慢，人右船左，人左船右。

3．mv1=Mv2任意时刻都成立，所以等式还可以成mX1=MX2。（X1和X2分别表示人和船相对水面的位移）

人船模型经典题型

1、质量为M的小船静止在湖面上，质量为m的人从船的左端走向船的右端，水的阻力不计，求船运动的距离？

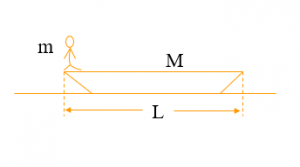
分析：以人和小船为系统最为研究对象，在整个过程中系统的动量守恒，整个系统总动量为零，人向右走的过程中，船也会向左移动。草稿图如下。

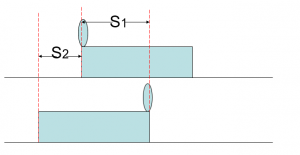
（S1表示人移动的距离，S2表示船移动的距离，S1+S2=L）

由 MV2=mV1时刻成立，得：MV2t=mV1t，整个过程中的时间等于无数t累加，V2t的累加等于S2，V1t的累加等于S1。

M S2=m S1

S1+S2=L

联立可解得：人的位移S1=ML/（M+m），船的位移S2=mL/（M+m）

2、光滑水平面上放有一表面光滑、倾角为α的斜面A，斜面质量为M、底边长为L，如图所示。将一质量为m、可视为质点的滑块B从斜面的顶端由静止释放，滑块B滑到斜面底端，求此过程中斜面向左滑动的距离？

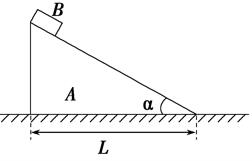
解析：由于A、B组成的系统水平方向不受外力，所以水平方向动量守恒，设A、B两者水平位移大小分别为x₁、x₂。

则Mv₁＝mv₂，x₁＝v₁t，x₂＝v₂t，x₁＋x₂＝L，解得x₁＝，

人船模型注意的问题

1．适用条件：

（1）系统由两个物体组成且相互作用前静止，系统总动量为零；

（2）在系统内发生相对运动的过程中至少有一个方向的动量守恒（如水平方向或竖直方向）且为零。

2．画草图：解题时要画出各物体的位移关系草图，找出各长度间的关系，注意两物体的位移是相对同一参考系的位移。

动量守恒定律经典题型（模型）

高中物理知识点总结

高中物理视频大全