
动量守恒定律是考试的重点对象,也是考试的难点,但考来考去常考的类型就只有那几类,动量守恒定律经典模型——碰撞中的动量守恒、子弹打木块和木块滑块中的动量守恒、人船模型、反冲和爆炸模型。
碰撞中的动量守恒模型
碰撞过程中动量守恒,考的最多的是两个小球之间的碰撞,如果是弹性碰撞,碰撞过程中机械能也守恒,例题如下:
质量为m1、m2的小球发生弹性正碰,如下图所示,m1有初速度V1,m2静止,求两小球碰撞后的速度
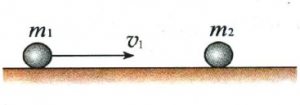
在碰撞的过程中机械能守恒和动量守恒。
动量守恒:![]()
机械能守恒:![]()
联立上面两式:
得碰撞后m1的速度:![]()
得碰撞后m2的速度:![]()
这是常考的一类动量守恒有关的模型,同学们不能只知道列等式,最好在理解的基础上把答案记住!
子弹打木块和木块滑块模型
在光滑的水平面上,子弹打木块的过程中,子弹和木块组成的系统动量守恒,例题如下:

1、质量为m的子弹以水平初速度Vo射入静止在光滑水平面上的滑块,滑块的质量为M,求射入以后滑块的速度为多大?
分析:以子弹和滑块为系统作为研究对象,整个过程中,系统动量守恒。
mVo=(m+M)V’
解得V’=mVo/(m+M)
扩展:这种类型的题目,考试往往不会单纯的考动量守恒定律,还会结合能量和做功方面进行考察,如要你计算在这个过程的能量损失,或者告诉你子弹与木块之间的作用力恒为f,要你求子弹射入木块的深度等等问题。
2、在光滑的水平面上有一静止的小车,小车足够长且表面粗糙,在小车的左端一滑块以初速度Vo滑上小车,求小车最初的速度为多大?
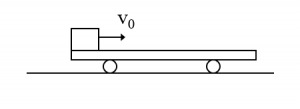
分析:以小车和滑块为系统作为研究对象,最终小车和滑块保持相对静止做匀速直线运动,整个过程中系统动量守恒。
mVo=(m+M)V’
解得V’=mVo/(m+M)
扩展:此题目还可以扩展一下,要你求系统产生的热量为多少?或者告诉你摩擦因数μ,需要你求滑块在小车上滑动的距离。
人船模型
人船模型是动量守恒定律模型中最让人难以的理解,因为运用了一点积分的思想,把距离和时间与速度联系,例题如下:
质量为M的小船静止在湖面上,质量为m的人从船的左端走向船的右端,水的阻力不计,求船运动的距离?
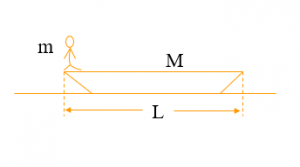
分析:以人和小船为系统最为研究对象,在整个过程中系统的动量守恒,整个系统总动量为零,人向右走的过程中,船也会向左移动。草稿图如下。
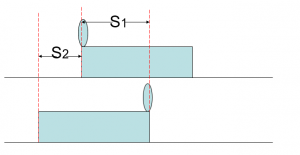
(S1表示人移动的距离,S2表示船移动的距离,S1+S2=L)
由 MV2=mV1时刻成立,得:MV2t=mV1t,整个过程中的时间等于无数t累加,V2t的累加等于S2,V1t的累加等于S1。
M S2=m S1
S1+S2=L
联立可解得:人的位移S1=ML/(M+m),船的位移S2=mL/(M+m)
反冲和爆炸模型
反冲和爆炸模型相对难度就小很多,题目一般较简单,例题如下:
1、一爆弹静止在光滑的水平面上,点燃后爆炸分为质量为m和M的两部分,质量为m的速度为v,求质量为M的部分速度为多大?
分析:爆弹在爆炸的过程中动量守恒,设爆炸后m的方向为正方向,爆弹作为研究系统。
由动量守恒:0=mv+MV’
解得V’=—mv/M(负号表示与规定的正方向相反)
2、静止的机关枪的质量为M,不断射出质量为m的n颗子弹,射出的速度为v,求最后机关枪的速度为多大?
分析:以机关枪和子弹为系统作为研究对象,在打出子弹的过程中动量守恒,设子弹的速度方向为正方向。
由动量守恒:0=nmv+MV’
解得:V’=—nmv/M(负号表示与规定的正方向相反)
动量守恒定律经典题型下载
高中物理知识点总结
One comment