
物块在凹槽里反复来回碰撞是比较喜欢考的一类压轴题,这类题目考察的知识点非常多,涉及到了动力学、动量守恒、功能关系等方面,以及对多物体运动过程分析方面知识,对学生分析问题和解决问题有较高的要求,刘叔物理借着这篇文章详细谈谈这方面的问题。
一、物块在凹槽里反复来回弹性碰撞的结论
内壁粗糙的凹槽在光滑的水平面上,凹槽中放一物块,现在给物块一瞬时初速度,物块开始运动到与凹槽刚相对静止所经历的时间等于物块不与凹槽发生碰撞直接减速到共速过程中经历的时间;如果给凹槽一瞬时初速度,结论一样成立。

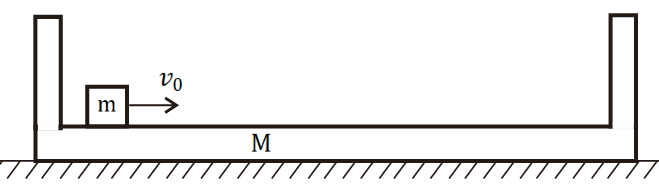
上面两种场景,第一个长木板足够长,第二个物块在凹槽里反复弹性碰撞,水平面光滑,摩擦因数相同,最后达到共速的时间相同。
原因解释:因为物块与凹槽碰撞为弹性碰撞,两者的速度不断向v_共靠近,直到两者速度等于v_共后相对静止匀速,根据弹性碰撞的基本结论,物块和凹槽碰撞前后速度关于共速的速度对称,速度差不变,所以时间等价于不发生碰撞直接减速到共速过程中经历的时间。
二、物块在凹槽里反复来回弹性碰撞的例题
1、如下图所示,光滑水平地面上有一静止的足够长的长木板,木板上有一滑块,现给滑块水平初速度v_0,长木板与物块间的动摩擦因数为μ,长木板质量为M,滑块质量为m,求从开始运动到长木板和滑块相对静止的过程中:

(1)经过的时间t
(2)长木板和滑块的位移。
解析:(1)由动量守恒:mv_0=(m+M)v_共
对m分析:μmg=ma,v_共=v_0-at
联立可解得:t=\cfrac{Mv_0}{(M+m)μg}
(2)长木板做匀加速直线运动,加速度a_板=\cfrac{μmg}{M}。
长木板运动的位移x_板=\cfrac{1}{2}\cfrac{μmg}{M}t^2=\cfrac{Mmv_0^2}{2μg(M+m)^2}。
滑块的位移x_块=\cfrac{(v_0+v_共)t}{2}=\cfrac{(2m+M)Mv_0^2}{2μg(M+m)^2}
2、如下图所示,在光滑水平地面上有一质量为M的凹槽,凹槽中放一质量为m的小物块,两者之间的动摩擦因数为μ,开始时两者静止,现给小物块以v_0初速度向右运动,设小物块与凹槽槽壁碰撞过程中没有能量损失,且碰撞时间不计,小物块可看成质点。求从小物块开始运动到两者刚相对静止所经历的时间。

解析:从凹槽开始运动到两者刚相对静止的过程中,设最后共速的速度为v_共,由动量守恒:mv_0=(m+M)v_共
对小物块与凹槽槽壁碰撞过程分析:小物块与凹槽槽壁碰撞为弹性碰撞,两者的速度不断向v_共靠近,直到两者速度等于v_共后相对静止匀速,根据弹性碰撞的基本结论,小物块和凹槽碰撞前后速度关于共速的速度对称。所以小物块开始运动到两者刚相对静止所经历的时间等于小物块速度从足够长的长木板上减速到v_共的时间,减速的加速度a=μg。
所以时间t=\cfrac{Mv_0}{(M+m)μg}
3、如下图所示,在光滑水平地面上有一凹槽A,中央放一小物块B,物块与左右两边槽壁的距离如图所示,L为1.0m,凹槽与物块的质量均为m,两者之间的动摩擦因数μ为0.05,开始时物块静止,凹槽以v_0=5m/s初速度向右运动,设物块与凹槽槽壁碰撞过程中没有能量损失,且碰撞时间不计。g取10m/s²。求:

(1)物块与凹槽相对静止时的共同速度;
(2)从凹槽开始运动到两者相对静止物块与右侧槽壁碰撞的次数;
(3)从凹槽开始运动到两者刚相对静止所经历的时间及该时间内凹槽运动的位移大小。
解析:(1)凹槽与物块组成的系统动量守恒:mv_0=2mv_共
相对静止时的共同速度v_共=\cfrac{v_0}{2}
(2)物块与凹槽间的滑动摩擦力f=μmg,设物块相对凹槽运动的路程为s
由功能关系:\cfrac{1}{2}mv_0^2=μmgs+\cfrac{1}{2}mv_共^2
代入数据可解得s=12.5m,由L=1.0m,得物块与右侧槽壁碰撞6次。
(3)从凹槽开始运动到两者刚相对静止所经历的时间等于凹槽由初速度v_0匀减速到v_共的时间。
v_0=v_共+μgt,可得时间t=5s
根据题意,物块与凹槽组成的系统开始质心位置在凹槽的中心位置;当物块相对凹槽静止后,物块在凹槽最左侧,此时物块与凹槽组成的系统质心位置在距离凹槽左侧\cfrac{L}{4}的位置。
物块与凹槽组成的系统不受外力作用,质心做匀速直线运动,质心速度v_c=\cfrac{v_0}{2}
质心在5s内运动的位移x_c=v_c t=\cfrac{v_0}{2}t
\cfrac{v_0}{2}t=\cfrac{x_物+x_槽}{2}。
由x_槽-x_物=\cfrac{L}{2}
联立可解得x_槽=12.75m
高中物理知识点总结