万有引力中椭圆轨道线速度的计算

在万有引力与航天章节中，我们知道行星绕中心天体做圆周运动的线速度大小计算方法

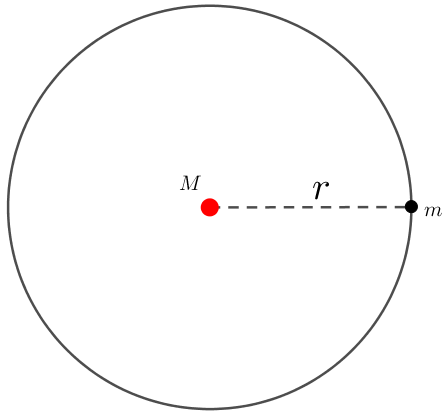
对m： $G\frac{Mm}{r^2}=m\frac{v^2}{r}$

可解得线速度大小： $v=\sqrt{\frac{GM}{r}}$

如果行星绕中心天体的运动是椭圆，那线速度大小该如何计算？刘叔物理先说明一下，这是竞赛内容，高中阶段不做要求，属于高考超纲内容，高考生可以直接下拉看最终结果。

如下图所示，质量为m的行星环绕质量为M的天体做椭圆运动，椭圆的半长轴为 $a$ ，半短轴为 $b$ ，设离M天体无穷远处引力势能为零，则离天体M距离为 $d$ 时引力势能 $E_p=-\cfrac{GMm}{d}$ 。

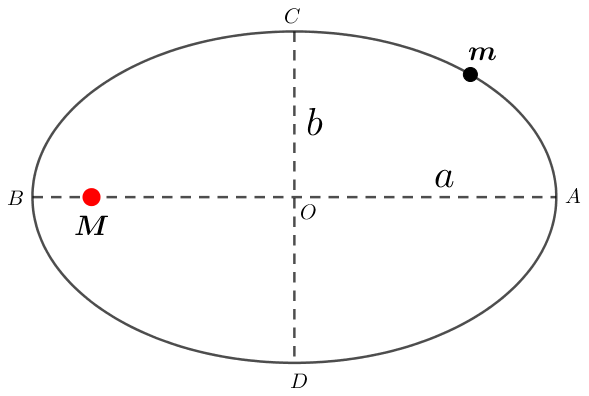
设A点的速率为 $v_A$ ，C点的速率为 $v_C$

在A、C两点由能量守恒可得：

E_总=-\cfrac{GMm}{a+c}+\cfrac{1}{2}m{v_A}^2=-\cfrac{GMm}{a}+\cfrac{1}{2}m{v_C}^2

在A、C两点根据开普勒第二定律： $v_C a\cos \theta =v_A(a+c)$

其中 $\cos \theta=\cfrac{b}{a}$

椭圆满足 $a^2=b^2+c^2$

可得： $E_总=-\cfrac{GMm}{2a}$

当行星 $m$ 距天体M为 $d$ 时，设此时的线速度为 $v$ ，由能量守恒可得：

-\cfrac{GMm}{2a}=-\cfrac{GMm}{d}+\cfrac{1}{2}m{v}^2

最后可得椭圆轨道线速度大小与距天体M的 $d$ 关系式：

v=\sqrt{\frac{2GM}{d}-\frac{GM}{a}}

高中物理知识点总结

高中物理视频大全