
在有关力学题目中,经常会碰到绳或杆关联的连接体问题,在高中阶段,大多数题目是求连接体速度情况的,但也有些模拟题让其判断加速度情况,但加速度的情况一般以定性分析为主,下面刘叔物理通过这篇文章,具体讨论一下绳或杆关联的连接体速度和加速度问题。
1、绳或杆关联的连接体速度问题讨论分析
这类问题在考试中经常碰到,处理方法基本就一条:将物体的速度沿着绳(杆)和垂直绳(杆)分解,两物体沿着绳(杆)的速度相等。
这样通用解法的本质原因:是因为我们把绳(杆)看成刚性的,绳(杆)不会收缩,两物体在沿着绳(杆)方向相对静止,从而在绳(杆)方向的速度相等。
高中阶段常见的绳或杆关联的连接体速度关系例子
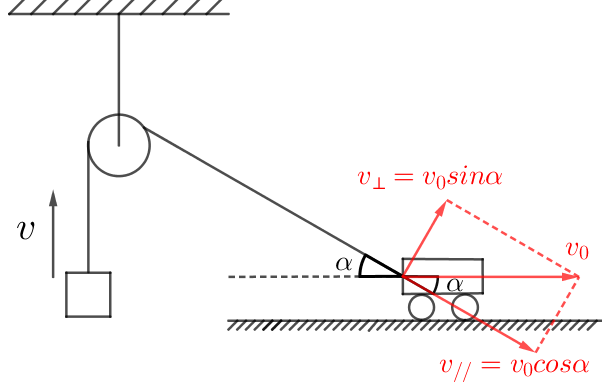
沿绳方向速度相等,v=v_0cosα
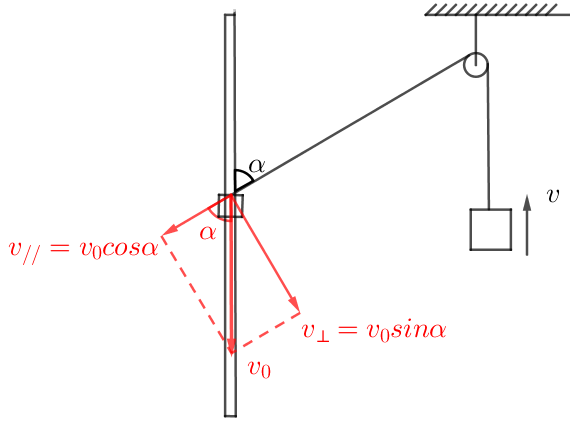
沿绳方向速度相等,v=v_0cosα
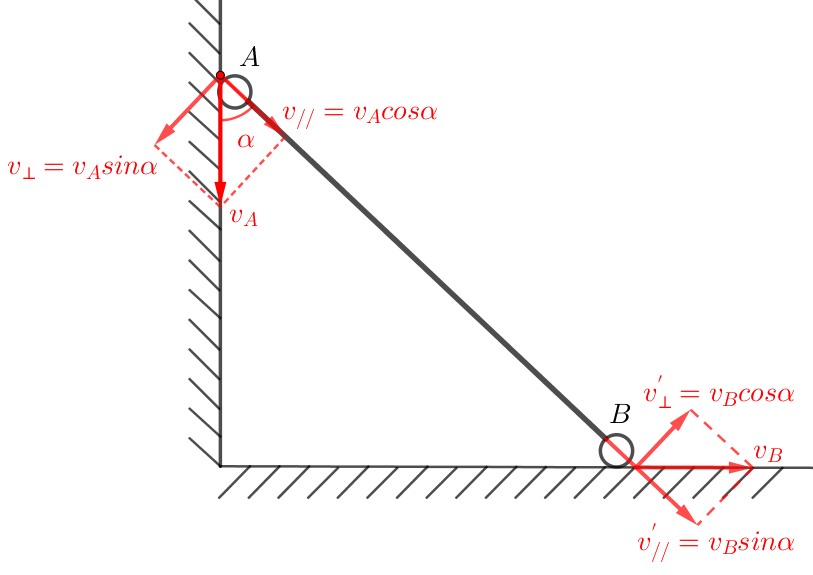
两小球沿杆方向速度相等,v_Acosα=v_Bsinα
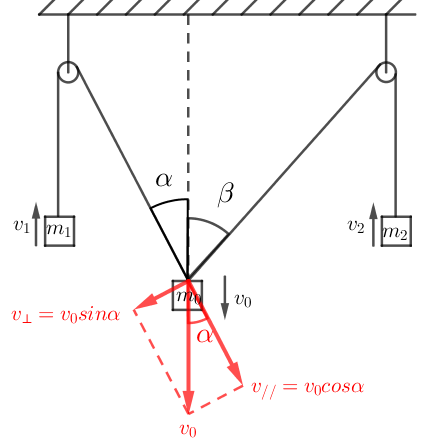
沿绳方向速度相等,v_1=v_0cosα
沿绳方向速度相等,v_2=v_0cosβ
2、绳或杆关联的连接体加速度问题讨论分析
绳或杆连接体的加速度问题相对比较复杂,高中物理一般不直接涉及加速度计算,偶尔会出现定性分析的题目。绳或杆连接体加速度问题一般分为两种情况:
(1)如果绳或杆连接体运动过程中只有平动,没有转动,那么连接体沿着绳或杆的加速度相等。
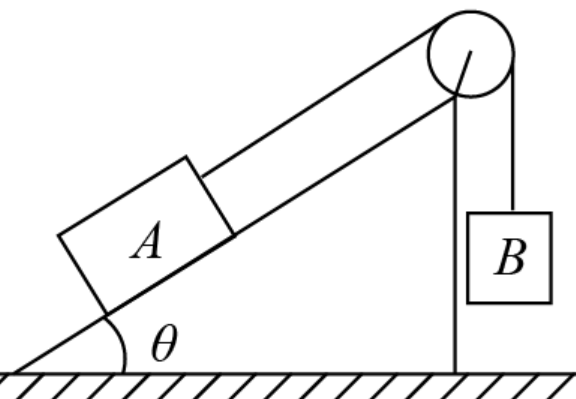
A、B两物体只有平动,没有转动,沿着绳方向加速度相等。
(2)如果绳或杆连接体运动过程中有平动,也有转动,那么连接体沿着绳或杆方向的加速度不相等。因为有转动,会有向心加速度的存在,这个时候需要考虑转动而产生的沿着绳或杆方向的向心加速度,下面刘叔物理具体列举一些常见的例子说明。
例子1:如下图所示的场景,物块和车通过绳关联,车的速度向右为v_0,物块的速度竖直向上为v,当绳与水平方向夹角为α时。

此时物块和车的速度关系满足:v=v_0cosα,那么两者的加速度满足怎样的关系呢?如果学过导数的话,可以直接将等式两边对时间求导。
上面等式两边对时间求导:a=a_0cosα+v_0(-sinα)( -ω)
其中ω=\cfrac{v_0 sinα}{L}=\cfrac{v_⊥}{L}
整理可得:a=a_0cosα+\cfrac{v_⊥^2}{L}
即:\red {a_0cosα=a-\cfrac{v_⊥^2}{L}}
其中v_⊥为车垂直绳方向的速度,L为滑轮到小车之间绳的长度。
可以看出,物块和车的加速度关系满足:车的加速度沿着绳方向的分量等于物块的加速度减去由于绳子转动产生的向心加速度。
例子2:如下图所示的场景,两物块通过绳关联,杆上物块的速度为v_0,右侧物块的速度竖直向上为v,当绳与竖直方向夹角为α时。

此时两物块的速度关系满足:v=v_0cosα
和上面一样的对两边求导,最后整理可得:\red {a_0cosα=a-\cfrac{v_⊥^2}{L}}
其中v_⊥为杆上物块垂直绳方向的速度,L为滑轮到杆上物块之间绳的长度。
可以看出,两物块的加速度关系满足:杆上物块的加速度沿着绳方向的分量等于右侧物块的加速度减去由于绳子转动产生的向心加速度。
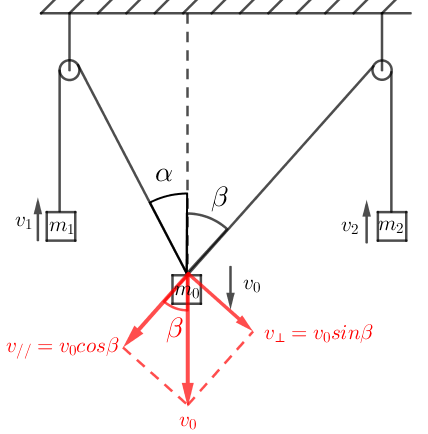
例子3:如下图所示的场景,三物块通过两个定滑轮和绳关联,相关的速度和角度如下图所示。

m_1和m_2通过绳关联,满足v_1=v_0cosα
上面等式两边对时间求导:a_1=a_0cosα+v_0(-sinα)( -ω)
整理可得:\red {a_0cosα=a_1-\cfrac{v_⊥^2}{L_1}}
其中v_⊥为m_0垂直绳方向的速度,L_1为左滑轮到m_0之间绳的长度。
可以看出,m_1和m_0的加速度关系满足:\red{m_0}的加速度沿着绳方向的分量等于\red{m_1}的加速度减去由于绳子转动产生的向心加速度。
同理可以得到m_2和m_0的加速度关系满足:\red {a_0cosα=a_2-\cfrac{v_⊥^2}{L_2}}
其中v_⊥为m_0垂直绳方向的速度,L_2为右滑轮到m_0之间绳的长度。
可以看出,m_2和m_0的加速度关系满足:\red{m_0}的加速度沿着绳方向的分量等于\red{m_2}的加速度减去由于绳子转动产生的向心加速度。
例子4:如下图所示的场景,A、B两小球通过轻杆关联,杆的长度为A的速度为L,v_A,B的速度为v_B,当杆与竖直方向夹角为α时。

此时A、B两小球速度关系满足:v_Acosα=v_Bsinα
上面等式两边对时间求导:a_A cosα+v_A(-sinα)ω=a_Bsinα+v_Bcosα ω
其中ω=\cfrac{v_Asinα+v_Bcosα}{L}
联立可得:\red{a_Bsinα=a_Acosα-\cfrac{(v_Asinα+v_Bcosα)^2}{L}}
可以看出,A、B两小球的加速度关系满足:B小球的加速度沿着杆方向的分量等于A小球的加速度沿着杆方向的分量减去杆转动产生的相对A小球的向心加速度。
实际上,对于连接体转动问题,放在极坐标下处理会比较方便,在处理时一般也是放在极坐标下的,极坐标下很容易明白有几个加速度以及加速度的物理意义,但极坐标系下速度与加速度的问题是竞赛内容,高中阶段不做要求。
高中物理知识点总结