
在高中阶段,高中物理经常会出现一类物体运动场景的题目,物体受到与速度方向相反大小与速度成正比的阻力下的运动,满足F_阻=kv,对于这种运动形式,高中生是很不好理解的,高考对这类题目也不做整个过程具体分析要求,基本上让求特殊位置的物理量,或者通过多告诉相关物理量,间接通过某种技巧性方式求所需要的,但这样导致的问题是让学生不能很好的理解这类问题,让学生有种似懂非懂的感觉,这次刘叔物理通过这篇文章,详细的介绍下这类问题,让同学们对这类问题有一个更加清晰的理解。文章会涉及简单的微积分,如果你是高中生看不懂,可以直接看结果,通过推导结果分析运动过程。
一、物体受到F=kv阻力下的运动分析
描述一个运动场景:如下图所示,质量为m的物块在光滑的水平面上,初速度大小为v_0,受到一个始终与速度方向相反、大小为kv阻力作用,分析运动过程中物块位移与时间关系、速度与时间关系、加速度与时间关系、速度与位移关系。
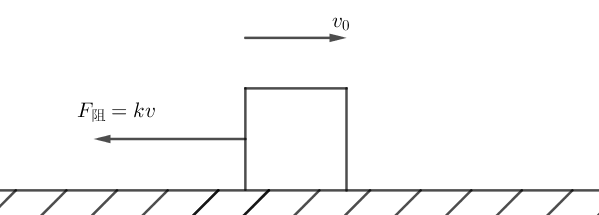
推导过程如下:
设v_0方向为正方向,对物块分析可得:kv=-ma,a=\cfrac{dv}{dt}
kv=-m\cfrac{dv}{dt}⇒\cfrac{1}{kv}=-\cfrac{dt}{mdv} \newline \cfrac{1}{kv}dv=-\cfrac{1}{m}dt (1)对(1)式两边积分:\int {\cfrac{1}{kv}dv}=-\int {\cfrac{1}{m}dt}
\cfrac{1}{k} lnv=-\cfrac{1}{m}t+C整理可得:v=e^{-\cfrac{k}{m}t+kC}
由初始条件t=0时,v=v_0,可得C=\cfrac{lnv_0}{k}
最后得到速度与时间关系\red {v=v_0e^{-\cfrac{k}{m}t}} (2)
由x=\int{vdt}=\int{v_0e^{-\cfrac{k}{m}t}}dt
x=-\cfrac{mv_0}{k}e^{-\cfrac{k}{m}t}+C由初始条件t=0时,x=0,可得C=\cfrac{mv_0}{k}
最后得到位移与时间关系\red {x=\cfrac{mv_0}{k}(1-e^{-\cfrac{k}{m}t})} (3)
对上面(2)两边求导可得加速度与时间关系:\red {a=-\cfrac{kv_0}{m}e^{-\cfrac{k}{m}t}} (4)
联立(2)(3)可得速度与位移关系:\red{v=v_0-\cfrac{k}{m}x} (5)
联立(3)(4)可得加速度与位移关系:\red {a=\cfrac{k^2}{m^2}x-\cfrac{k}{m}v_0}(6)
结论:受合力为kv阻力的物体,速度随位移均匀变化,速度与位移成线性关系;物块的合外力随位移均匀变化,合外力与位移成线性关系。物体的速度随位移均匀变化的直线运动一般称为另类的匀变速直线运动。
二、物体受到F=kv阻力下的运动变式——单棒无外力切割磁感线的运动
如下图所示,水平导轨光滑,导轨宽为L,电阻为R,给导体棒以水平初速度v_0。

对导体棒受力分析,所受的水平向左的安培力F=\cfrac{B^2L^2v}{R},很明显可以看出,导体棒受到的安培阻力与速度成正比,满足F=kv的形式,其中k=\cfrac{B^2L^2}{R}
通过上面分析的结论可知:导体棒的速度与位移成线性关系,速度随位移均匀减小,通过相等的位移速度减小量相等,导体棒做另类的匀变速直线运动。
导体棒速度与时间关系:\red {v=v_0e^{-\cfrac{B^2L^2}{mR}t}}
导体棒速度与位移关系:\red{v=v_0-\cfrac{B^2L^2}{mR}x}
三、物体受到F=kv阻力下的运动变式——下落物体受到kv阻力作用下的运动。
如下图所示,质量为m的小球距离地面足够高,静止开始下落,下落过程中受到始终与速度方向相反大小等于kv的阻力作用。
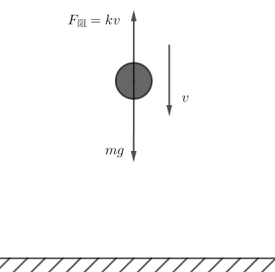
对小球受力分析:mg-kv=ma⇒mg-kv=m\cfrac{dv}{dt}
分离变量:\cfrac{1}{m}dt=\cfrac{1}{mg-kv}dv
两边积分:\int{\cfrac{1}{m}dt}=\int{\cfrac{1}{mg-kv}dv}
积分结果:\cfrac{t}{m}+C=-\cfrac{1}{k}\ln (mg-kv)
初始条件:当t=0时,v=0,可得C=-\cfrac{1}{k} \ln mg
化简整理得:\red {v=\cfrac{mg}{k}(1-e^{-\cfrac{k}{m}t})} (1)
由上式可得:\cfrac{dx}{dt}=\cfrac{mg}{k}(1-e^{-\cfrac{k}{m}t})
分离变量:\cfrac{k}{mg}dx=(1-e^{-\cfrac{k}{m}t})dt
两边积分:\int {\cfrac{k}{mg}dx}=\int {(1-e^{-\cfrac{k}{m}t})dt}
积分结果:\cfrac{k}{mg}x+C=t+\cfrac{m}{k}e^{-\cfrac{k}{m}t}
初始条件:当t=0时,x=0,可得C=\cfrac{m}{k}
化简整理得:\red {x=\cfrac{mg}{k}t+\cfrac{m^2g}{k^2}(e^{-\cfrac{k}{m}t}-1)}(2)
由(1)式可知e^{-\cfrac{k}{m}t}-1=-\cfrac{kv}{mg}
代入(2)式整理可得:\red{x=\cfrac{m}{k}[\cfrac{mg}{k}\ln(\cfrac{mg}{mg-kv})-v]}(3)
从(3)式可以看出,物体除了受kv阻力的作用,如果有其他恒力提供动力,运动速度随位移不是均匀变化。
四、电磁感应中无动力的双杆切割磁感线问题
2024年高考,双杆切割是一个很大的热门,有不少省份压轴题考的就是无动力的双杆切割磁感线问题,比如江西卷和湖北卷等,借着这篇文章,刘叔物理详细分析一下无动力的双杆切割问题。
如下图所示,水平面内有两根足够长的光滑导轨,导轨间距为L,导轨平面有垂直纸面向里的磁场,磁感应强度大小为B,两根相同的光滑导体棒1、2放在导轨上,质量为m,导体棒长为L,两导体棒相距足够远,导轨电阻不计,两导体棒的总电阻为R_总,现给其中一导体棒水平初速度v_0,导体棒1、2从开始运动到达到稳定状态的过程中。
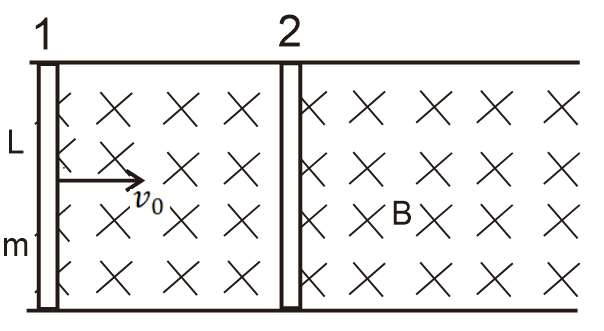
问:
(1)整个过程中导体棒1、2做什么运动?
(2)求整个过程产生的热量?
(3)求整个过程中导体棒1、2的相对位移?
(4)求整个过程中流过导轨的电荷量是多少?
解析:(1)导体棒1先做加速度减小的减速运动,后做匀速运动;导体棒2先做加速度减小的加速运动,后做匀速运动。导体棒1、2最后相对静止,一起做匀速直线运动。
(2)分析可知导体棒1、2组成的系统动量守恒:mv_0=2mv_共
根据能量守恒:Q=\cfrac{1}{2}m{v^2}_0-\cfrac{1}{2}2m{v^2}_共=\cfrac{1}{4}m{v^2}_0
(3)对导体棒1、2分别用动量定理。
对导体棒1:-\cfrac{B^2L^2}{R_总}\sum ΔvΔt=mv_共-mv_0
对导体棒2:\cfrac{B^2L^2}{R_总}\sum ΔvΔt=mv_共
可解得:v_共=\cfrac{v_0}{2},相对位移x=\sum ΔvΔt=\cfrac{mv_0R_总}{2B^2L^2}
(4)回路中流过的电荷量Q=It=\cfrac{BL}{R_总}\sum ΔvΔt=\cfrac{mv_0}{2BL}
下面刘叔物理推导一下导体棒1、2的速度与时间关系、位移与时间关系、速度与位移关系。

对导体棒1:-\cfrac{B^2L^2}{R_总}(v_1-v_2)=ma_1=m\cfrac{dv_1}{dt}(4)
对导体棒2:\cfrac{B^2L^2}{R_总}(v_1-v_2)=ma_2=m\cfrac{dv_2}{dt}(5)
可得:-m\cfrac{dv_1}{dt}=m\cfrac{dv_2}{dt}⇒-dv_1=dv_2
两边积分:\int{-dv_1}=\int{dv_2}⇒-v_1=v_2+C
代入初始条件v_1=v_0,v_2=0得C=-v_0,即v_0=v_1+v_2(6)
将(6)式代入(4)式消去v_2可得:-\cfrac{B^2L^2}{R_总}(2v_1-v_0)=m\cfrac{dv_1}{dt}
分离变量:-\cfrac{B^2L^2}{mR_总}dt=\cfrac{1}{2v_1-v_0}dv_1
两边积分:-\cfrac{B^2L^2}{mR_总}\int{dt}=\int{\cfrac{1}{2v_1-v_0}dv_1}
可得:-\cfrac{B^2L^2}{mR_总}t+C=\cfrac{1}{2}\ln(2v_1-v_0)
初始条件满足t=0,v_1=v_0,可得C=\cfrac{1}{2}\ln{v_0}
整理得:\red{v_1=\cfrac{v_0}{2}(1+e^{-\cfrac{2B^2L^2}{mR_总}t})}
代入v_0=v_1+v_2可得:\red{v_2=\cfrac{v_0}{2}(1-e^{-\cfrac{2B^2L^2}{mR_总}t})}
同理可得位移与时间关系:
\red{x_1=\cfrac{mv_0R_总}{4B^2L^2}(\cfrac{2B^2L^2}{mR_总}t-e^{-\cfrac{2B^2L^2}{mR_总}t}+1)}\newline \newline \red{x_2=\cfrac{mv_0R_总}{4B^2L^2}(e^{-\cfrac{2B^2L^2}{mR_总}t}+\cfrac{2B^2L^2}{mR_总}t-1)}同理可得位移与速度关系:
\red{x_1=\cfrac{mv_0R_总}{4B^2L^2}[2-\ln (\cfrac{2v_1}{v_0}-1)-\cfrac{2v_1}{v_0}]} \newline \red{x_2=-\cfrac{mv_0R_总}{4B^2L^2}[\ln (1-\cfrac{2v_2}{v_0})+\cfrac{2v_2}{v_0}]}高中物理知识点总结